
If the universe speaks, it does so in the language of mathematics. Throughout human history, a few brilliant minds have managed to decipher fragments of this cosmic code, condensing profound truths about nature into simple, elegant lines of symbols. These are the equations that changed the world.
They are far more than dusty formulas in a textbook; they are the stories of human curiosity and discovery, the keys that unlocked new realms of science, and the fundamental blueprints for our technological civilization. From the triangle that grounds our architecture to the quantum wave that powers our computers, these equations form an invisible framework that underpins our reality. In this article, we'll journey through 17 of these monumental formulas, demystifying the symbols to reveal the revolutionary ideas they contain and the immense impact they have had on the course of history.
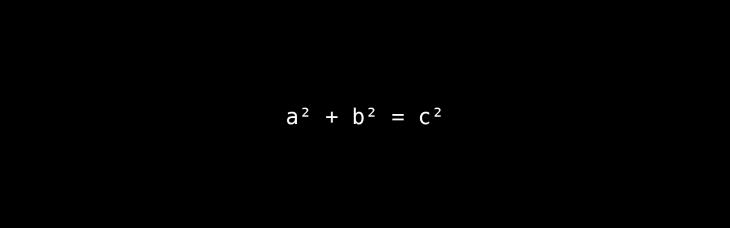
The Core Idea: This equation provides a fundamental relationship between the three sides of a right-angled triangle, linking geometry and algebra.
A Deeper Look & Analogy: The equation isn't just about lengths; it's a statement about areas. Imagine you build a square on each of the triangle's three sides. Pythagoras's theorem states that the area of the largest square (the one built on the hypotenuse, c) is exactly equal to the sum of the areas of the two smaller squares (built on sides a and b). It's a perfect, elegant balance.
The Architect & The Era: While credited to the Greek mathematician Pythagoras (c. 530 BC), the concept was known to earlier civilizations like the Babylonians and Egyptians. However, Pythagoras and his school are credited with providing the first formal proof, elevating it from a practical observation to a universal mathematical truth.
Lasting Impact: Beyond being the first thing most people learn in geometry, this theorem is the cornerstone of how we measure physical space. It's essential for architecture, surveying land, and navigation. More advanced applications include triangulation, the method your phone's GPS uses to pinpoint your location by calculating its distance from multiple satellites. It represents a foundational leap from simple arithmetic to the abstract world of geometry.
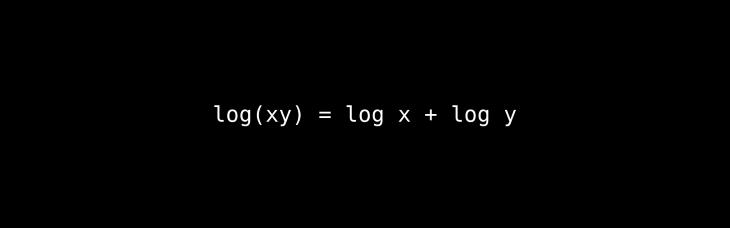
The Core Idea: Logarithms are a clever way to simplify difficult calculations by transforming multiplication into addition and division into subtraction.
A Deeper Look & Analogy: Think of logarithms as a "language of exponents." If 102=100, then the logarithm (base 10) of 100 is 2. Logarithms "undo" exponentiation. The rule log(xy)=log(x)+log(y) was revolutionary because adding two numbers is vastly easier and less error-prone than multiplying them, especially when dealing with the huge numbers found in astronomy.
The Architect & The Era: The concept was developed by John Napier in 1610. He spent decades creating tables of logarithms by hand, a monumental effort to aid astronomers in their calculations of planetary motion.
Lasting Impact: Logarithms were the "calculators" of their day for nearly 300 years. The slide rule, an essential tool for engineers and scientists until the 1970s, is a physical embodiment of logarithmic scales. Today, logarithmic scales are still used to measure quantities that span huge ranges, such as the Richter scale for earthquakes, decibels for sound, and the pH scale for acidity.
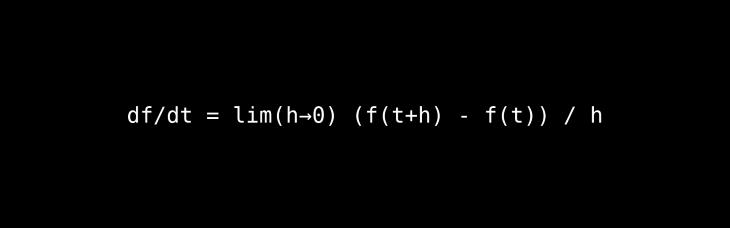
The Core Idea: This formula, the definition of a derivative, gives us a way to calculate the instantaneous rate of change.
A Deeper Look & Analogy: Imagine you're driving a car. Your average speed is the total distance divided by the total time. But what is your exact speed at the precise moment you look at the speedometer? That's what the derivative calculates. It finds the slope (rate of change) of a curve at a single, infinitely small point by looking at the slope between two points that are brought infinitesimally close together (as h approaches 0).
The Architect & The Era: Calculus was developed independently by Isaac Newton (1668) and Gottfried Leibniz in the late 17th century. Newton developed it to describe planetary motion and gravity, while Leibniz developed the superior notation we still use today.
Lasting Impact: Calculus is arguably the most powerful mathematical tool ever invented. It's the language of motion, change, and optimization. It's used in physics to describe velocity and acceleration, in economics to find maximum profit, in engineering to design optimal structures, and in medicine to model the growth of tumors. It's an essential pillar of modern science and technology.
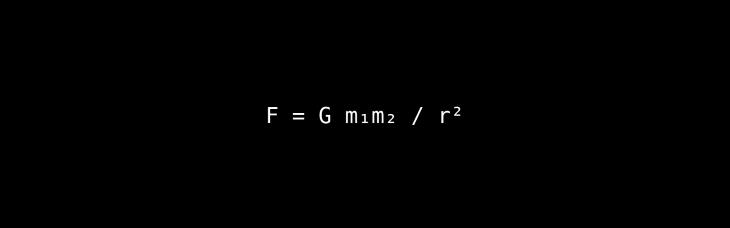
The Core Idea: This law describes the force of attraction between any two objects in the universe.
A Deeper Look & Analogy: The most important part of this formula is the inverse-square relationship (r2 in the denominator). This means that the force of gravity weakens dramatically with distance. If you double the distance between two objects, the gravitational force between them drops to one-quarter (1/22) of its original strength. Triple the distance, and the force drops to one-ninth (1/32). This precise relationship is why planetary orbits are stable ellipses and not chaotic spirals.
The Architect & The Era: Isaac Newton (1687) published this in his Principia Mathematica. His genius was not in noticing gravity, but in proposing a universal law that was mathematically precise and applied to everything from a falling apple to the orbit of the Moon.
Lasting Impact: This single equation governed physics for over 200 years. It allowed astronomers to predict the existence of the planet Neptune before it was ever observed, based on its gravitational pull on Uranus. Today, it remains essential for calculating trajectories for satellites and interplanetary probes. It was the first truly universal physical law.
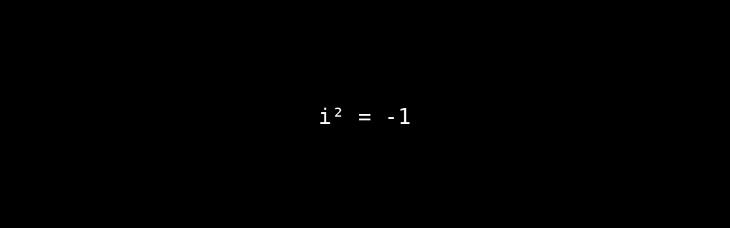
The Core Idea: This defines the "imaginary unit" i, which is the foundation of complex numbers.
A Deeper Look & Analogy: Mathematicians were long stumped by equations that required finding the square root of a negative number. Leonhard Euler (1750) championed the idea of simply defining a new number, i, to be the solution. Complex numbers have two parts: a real part and an imaginary part (e.g., 3+2i). They can be visualized on a 2D plane, which allows them to represent rotations and oscillations in a uniquely powerful way.
The Architect & The Era: While the concept had been toyed with for centuries, Leonhard Euler was instrumental in integrating it into mainstream mathematics.
Lasting Impact: The term "imaginary" is a misnomer; these numbers are critical for describing very real phenomena. Electrical engineering is almost impossible without them, as they simplify calculations involving alternating currents. They are also at the heart of quantum mechanics (Schrödinger's Equation) and are used in signal processing for everything from radar to Wi-Fi.
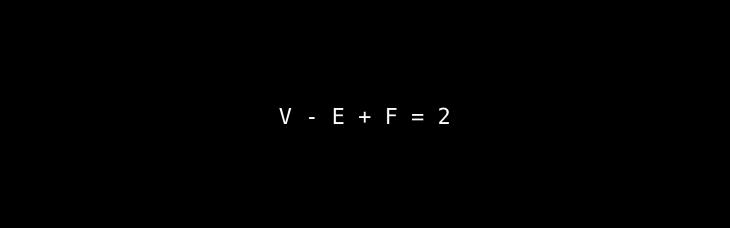
The Core Idea: This simple formula reveals a hidden, fundamental property of all simple three-dimensional solids with flat faces.
A Deeper Look & Analogy: Take any simple polyhedron—a cube, a pyramid, a soccer ball. Count its vertices (corners, V), edges (E), and faces (F). No matter how you stretch, bend, or deform the shape (without tearing it), the quantity V−E+F will always remain 2. A cube has 8 vertices, 12 edges, and 6 faces: 8−12+6=2. A pyramid with a square base has 5 vertices, 8 edges, and 5 faces: 5−8+5=2.
The Architect & The Era: Leonhard Euler (1751) discovered this property, which was a foundational step in the field of topology.
Lasting Impact: Topology is like "rubber sheet geometry"—it studies the properties of shapes that are preserved under continuous deformation. This formula was one of the first topological invariants ever discovered. It marked a shift from studying rigid properties like length and angle to studying more fundamental properties like connectivity, which is crucial for modern fields like network theory and computer graphics.

The Core Idea: This equation describes the ubiquitous bell-shaped curve that represents the distribution of many random variables.
A Deeper Look & Analogy: Think about the heights of all men in a country. Most will be clustered around the average height. There will be fewer very tall men and fewer very short men. If you graph this, you get a bell curve. The formula, though complex-looking, precisely draws that shape based on the mean (μ) and standard deviation (ρ), which measures the "spread" of the data.
The Architect & The Era: The concept was first introduced by Abraham de Moivre, but it was rigorously developed by Carl Friedrich Gauss (1810) as he analyzed astronomical measurement errors.
Lasting Impact: The normal distribution is the cornerstone of modern statistics. It allows us to determine if the results of a medical trial are statistically significant or just due to random chance. It's used in finance to model stock returns, in manufacturing for quality control, and in social sciences to analyze survey data. It gives us a powerful tool to find signals in a world full of noise.
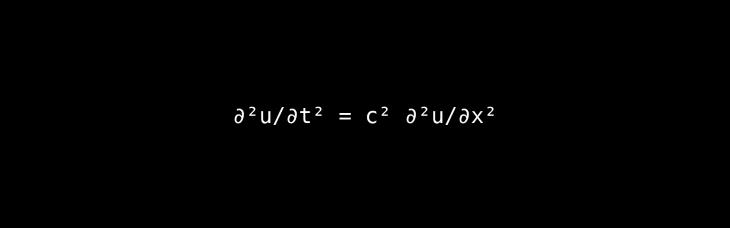
The Core Idea: This equation is the master blueprint for describing how waves propagate through space and time.
A Deeper Look & Analogy: The equation relates two different kinds of change. The left side (∂t2∂2u) represents the acceleration of a point on the wave (how its motion changes over time). The right side (∂x2∂2u) represents the curvature of the wave (how it changes over space). The equation states that the acceleration of a point is proportional to its curvature. A highly curved part of a wave (like a sharp crest) will accelerate downwards rapidly, which is what makes the wave move.
The Architect & The Era: Jean d'Alembert (1746) was the first to formulate this equation for a vibrating string, a key problem of the 18th century.
Lasting Impact: This mathematical form is incredibly versatile. Modified versions of it describe the behavior of sound waves (acoustics), light waves (electromagnetism), water waves (fluid dynamics), and even the vibrations in a bridge or building (structural engineering). It's a universal law for anything that wiggles and travels.
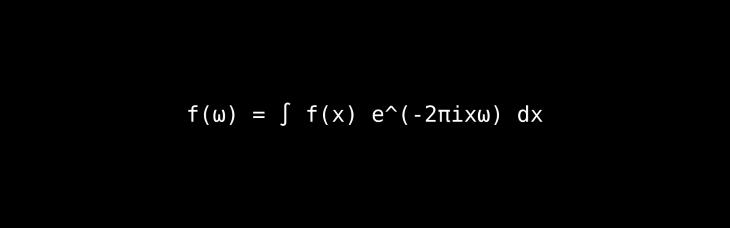
The Core Idea: A mathematical technique for decomposing any complex signal into a sum of simple, pure sine waves.
A Deeper Look & Analogy: Imagine you hear a chord played by an orchestra. Your ear hears it as one complex sound. The Fourier transform is like a super-powered ear that can tell you exactly which instruments played which notes, at what loudness. It transforms a signal from the time domain (how it changes over time) to the frequency domain (what frequencies it's made of).
The Architect & The Era: Joseph Fourier (1822) developed this technique while studying heat flow, showing that even complex heat distributions could be represented as a sum of simple waves.
Lasting Impact: The Fourier transform is the heart of the digital world. It's the basis for data compression: JPEG compression works by throwing away the "high-frequency" visual information that our eyes don't easily notice, and MP3 does the same for sound. It's also used to clean up signals in medical imaging (MRI) and analyze seismic data to find oil.
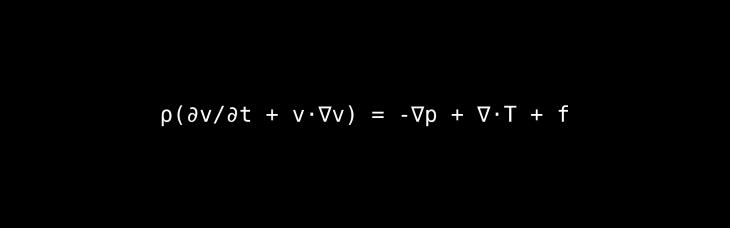
The Core Idea: This set of equations describes the motion of viscous fluids, like water, air, or honey.
A Deeper Look & Analogy: This is essentially Newton's second law (F=ma) for fluids, but it's far more complex because a fluid is a continuous medium. The equation has to account for multiple forces at once: changes in pressure (which pushes the fluid), viscosity (internal friction, or how "thick" the fluid is), and external forces like gravity. Its complexity arises from its "non-linearity," which is why fluid motion can become turbulent and chaotic.
The Architect & The Era: Developed by Claude-Louis Navier and George Gabriel Stokes over the first half of the 19th century, building on Euler's earlier work with ideal fluids.
Lasting Impact: These equations are critical for nearly every field involving fluid motion. They are used to design more aerodynamic airplanes and cars, predict weather patterns and climate change, model the flow of blood through the circulatory system, and design efficient pipelines. Solving these equations is so difficult that a $1 million prize is offered for proving certain mathematical properties about their solutions.
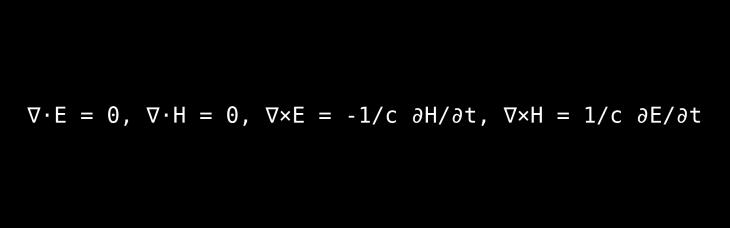
The Core Idea: A set of four elegant equations that completely describe the behavior of electricity, magnetism, and light.
A Deeper Look & Analogy: These equations reveal a beautiful symmetry in nature. They show that:
Electric charges create electric fields.
There are no magnetic monopoles (magnets always have a north and south pole).
A changing magnetic field creates an electric field (the principle behind electric generators).
An electric current and a changing electric field create a magnetic field. The last two points show that a change in one field can create the other. This self-perpetuating dance creates an electromagnetic wave that travels at the speed of light—because it is light.
The Architect & The Era: James Clerk Maxwell (1865) unified centuries of experimental work by Faraday, Ampère, and Gauss into this single, cohesive theory.
Lasting Impact: This was one of the most significant achievements in the history of science. It directly predicted the existence of radio waves, paving the way for all modern wireless communication: radio, television, radar, Wi-Fi, and cell phones. It's the complete classical theory for all of electromagnetism.
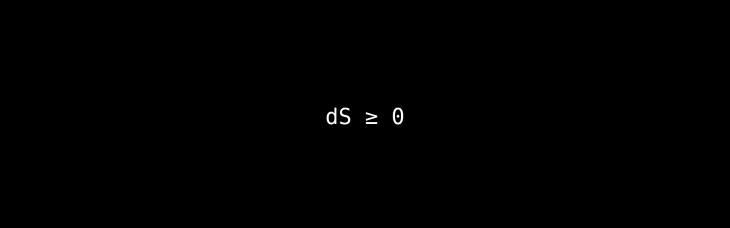
The Core Idea: This law states that the total entropy (a measure of disorder or randomness) of an isolated system can never decrease over time.
A Deeper Look & Analogy: Think of your bedroom. It takes energy and effort to keep it tidy (low entropy). If left alone (as an isolated system), it will naturally tend toward a state of messiness (high entropy). This law is why a hot cup of coffee cools down in a room (the heat energy disperses in a more "disordered" way) but a room-temperature coffee never spontaneously heats up by drawing heat from the air. This directionality gives us the "arrow of time."
The Architect & The Era: The concept was developed throughout the 19th century, but the formulation is heavily associated with Ludwig Boltzmann (1874), who connected entropy to the statistical behavior of atoms.
Lasting Impact: The second law is one of the most fundamental principles in all of physics. It sets a hard limit on the efficiency of engines and power plants. It explains why chemical reactions proceed in one direction and not the other, and it even has profound philosophical implications for the ultimate fate of the universe (the "heat death" scenario, where all energy is evenly distributed and no useful work can be done).
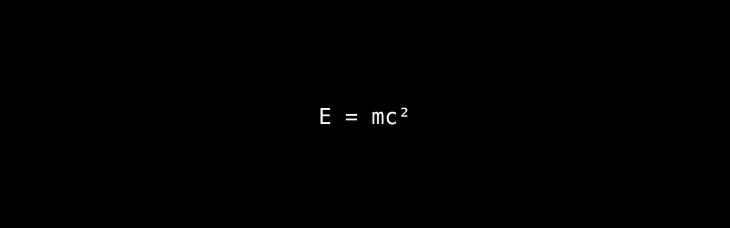
The Core Idea: This equation reveals the astonishing equivalence of mass and energy.
A Deeper Look & Analogy: This formula is a consequence of Einstein's theory of special relativity. It states that mass is a highly concentrated form of energy. The conversion factor, c2 (the speed of light squared), is an enormous number. This means that converting even a tiny amount of mass into pure energy releases a catastrophic amount of it. It's like discovering that a single penny contains the energy of a massive power plant.
The Architect & The Era: Albert Einstein published this as part of his theory of special relativity in 1905, a year often called his "miracle year."
Lasting Impact: This equation explains the power source of the stars: they shine by converting mass into energy through nuclear fusion. It is also the principle behind both nuclear power, which harnesses this energy in a controlled way, and nuclear weapons, which release it all at once. It fundamentally changed our understanding of matter and energy.
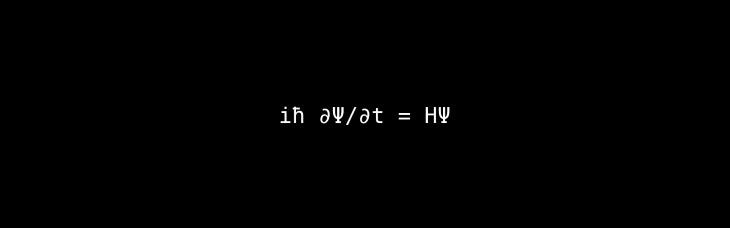
The Core Idea: This is the central equation of quantum mechanics, describing how the quantum state of a particle evolves over time.
A Deeper Look & Analogy: In the quantum world, particles like electrons don't have a definite position until they are measured. Instead, they exist in a "superposition" of all possible states, described by a wave function (Ψ). Think of the wave function as a "cloud of probability." The Schrödinger equation is the rulebook that governs how this probability cloud moves, spreads out, and changes its shape over time.
The Architect & The Era: Erwin Schrödinger (1927) formulated this equation to describe the wave-like behavior of electrons in atoms.
Lasting Impact: Virtually all modern technology is based on our understanding of quantum mechanics, and this equation is its foundation. It made it possible to understand chemical bonds, predict the properties of materials, and develop technologies like semiconductors, transistors (the basis of all computers), lasers, and medical imaging.
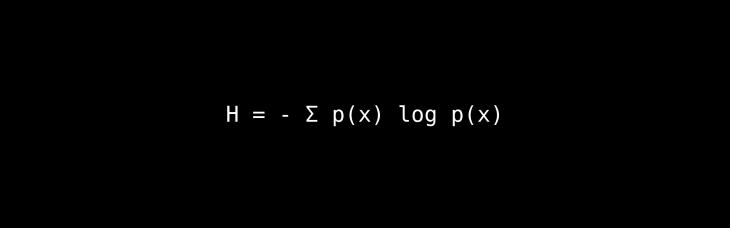
The Core Idea: This equation, known as Shannon entropy, provides a precise mathematical way to measure the amount of information in a message.
A Deeper Look & Analogy: The equation defines information in terms of unpredictability or surprise. A message with a predictable outcome (like the result of a weighted coin that lands on heads 99% of the time) has very little information. A message with an unpredictable outcome (like the result of a fair coin flip) has more information. The formula calculates the average amount of "surprise" you can expect from a source of data.
The Architect & The Era: Claude Shannon (1949), a brilliant mathematician and engineer, single-handedly founded the field of information theory with his groundbreaking paper.
Lasting Impact: Shannon's work is the mathematical bedrock of the entire digital revolution. It established the absolute limits for data compression (how small a file can be zipped) and for reliable data transmission over a noisy channel (how fast your internet connection can be). Every time you stream a video, send an email, or use your phone, you are relying on the principles of information theory.

The Core Idea: This simple equation, the logistic map, demonstrates that very simple, deterministic systems can produce incredibly complex and unpredictable behavior.
A Deeper Look & Analogy: This equation can be used to model population growth. xt is the population this year (as a fraction of the maximum possible), and xt+1 is the population next year. Depending on the value of the growth rate parameter k, the population might stabilize, oscillate between a few values, or become completely chaotic and unpredictable. This sensitivity to the initial conditions is known as the "butterfly effect": a butterfly flapping its wings in Brazil could theoretically set off a chain of events that leads to a tornado in Texas.
The Architect & The Era: The field of chaos theory was pioneered by figures like Edward Lorenz in meteorology, but Robert May's 1975 paper on this simple map was hugely influential.
Lasting Impact: Chaos theory revolutionized science by showing the limits of prediction. It helped explain why long-term weather forecasting is fundamentally impossible. It has found applications in modeling stock market fluctuations, the dynamics of heart arrhythmias, and the flow of traffic. It revealed that randomness can emerge from simple, non-random rules.
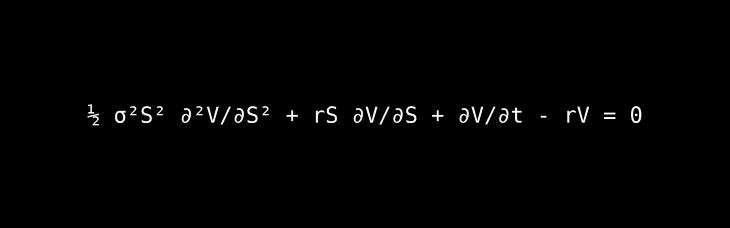
The Core Idea: This equation provides a model for calculating the fair price of a financial option.
A Deeper Look & Analogy: An "option" is a contract that gives you the right, but not the obligation, to buy or sell a stock at a set price in the future. Pricing this right is incredibly tricky because the stock's future value is unknown. The Black-Scholes equation is like a very sophisticated recipe that combines several ingredients—the current stock price, the option's strike price, the time until expiration, the risk-free interest rate, and the stock's volatility (how much its price tends to swing)—to cook up a fair price for the option today.
The Architect & The Era: Developed by Fischer Black and Myron Scholes (with contributions from Robert Merton) in the early 1970s, for which Scholes and Merton later received the Nobel Prize in Economics.
Lasting Impact: This equation transformed finance from a gut-instinct-driven field to a highly mathematical one. It created a standardized way to price and trade the vast and complex world of financial derivatives. This fueled an explosion in the financial markets, allowing for more sophisticated risk management but also contributing to the complexity that played a role in the 2008 financial crisis.